Budowa kwadratów nieparzysto-parzystych
Jak już zaznaczyliśmy, najmniej istnieje przepisów dotyczących budowy tego typu kwadratów, a przy tym wszystkie metody są skomplikowane i trudne do zapamiętania. Przytaczamy tu względnie najłatwiejszą, której twórcą jest La Hire; ale i ona daleka jest od wytworności pomysłu, jaka cechuje metody podane uprzednio. Postępując podobnie jak przy kwadratach parzysto-parzystych, budujemy kwadraty pomocnicze: pierwszy z postępu 1, 2, 3, 4, 5, 6, drugi z postępu 0, 6, 12, 18, 24, 30. Oba te kwadraty nie są magiczne, ale ich przekątne dają sumę magiczną. Gdy kwadraty te zsumujemy, również nie otrzymamy jeszcze kwadratu magicznego.
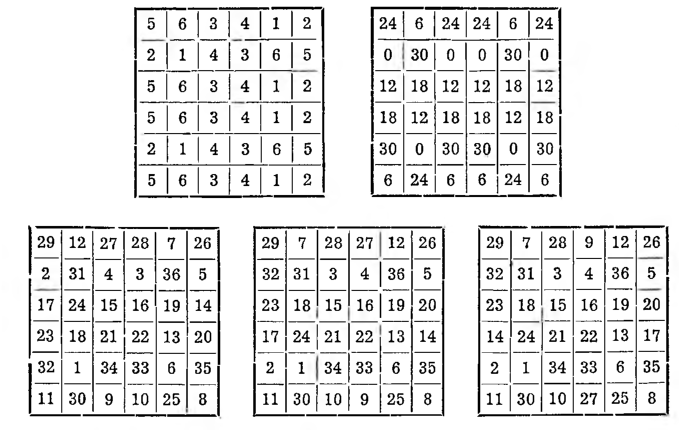 Otrzymać go możemy dopiero po serii przestawień, mianowicie: pozostawiając na miejscu liczby idące po przekątnej, przestawiamy w pierwszym od góry rzędzie i w pierwszej z lewa kolumnie odpowiadające sobie wzajemnie miejscami liczby 12 i 7, 27 i 28, 2 i 32, 17 i 23. W drugimi i w ostatnim rzędzie przestawiamy: 4 i 3, 9 i 10. W drugiej i w ostatniej kolumnie: 24 i 18, 14 i 20, Wyniknie z tego czwarty, podany tu kwadrat, w którym przestawić jeszcze należy liczby czwartego rzędu i czwartej kolumny: 17 i 14, 27 i 9. Otrzymamy wówczas kwadrat piąty, który jest wreszcie kwadratem magicznym z sumą magiczną 111.
Otrzymać go możemy dopiero po serii przestawień, mianowicie: pozostawiając na miejscu liczby idące po przekątnej, przestawiamy w pierwszym od góry rzędzie i w pierwszej z lewa kolumnie odpowiadające sobie wzajemnie miejscami liczby 12 i 7, 27 i 28, 2 i 32, 17 i 23. W drugimi i w ostatnim rzędzie przestawiamy: 4 i 3, 9 i 10. W drugiej i w ostatniej kolumnie: 24 i 18, 14 i 20, Wyniknie z tego czwarty, podany tu kwadrat, w którym przestawić jeszcze należy liczby czwartego rzędu i czwartej kolumny: 17 i 14, 27 i 9. Otrzymamy wówczas kwadrat piąty, który jest wreszcie kwadratem magicznym z sumą magiczną 111.
Przemieszczenia te sprowadzić się dają do trzech reguł ogólnych. Nie ruszając liczb stojących na przekątnych przestawia się kolejno:
1° — w pierwszym rzędzie i w pierwszej kolumnie liczby pól wzajemnie sobie odpowiadających;
2° — w drugim i w ostatnim rzędzie oraz w drugiej i ostatniej kolumnie — liczby pól środkowych;
3° — w jednym z rzędów środkowych i -w jednej ze środkowych kolumn — liczby pól skrajnych.
Można oczywiście zamiast pierwszego rzędu i pierwszej kolumny wziąć ostatni rząd i ostatnią kolumnę, można również i przestawienia 2° i 3° modyfikować, byle nie tknąć liczb na polach biegnących po przekątnej.
Budując kwadrat magiczny przy pomocy kwadratów pomocniczych można sobie uplanować, że w pewnym polu znajdzie się pewna liczba, i względnie łatwo to osiągnąć. Na przykład, gdy zechcemy, by w polu środkowym znalazła się jedynka, wówczas od tego pola rozpoczynamy budowę kwadratu pierwszego i wstawiamy tam 1, w drugim zaś kwadracie zabiegamy o to, by w tymże polu wypadło 0.