
Nie mam chwilowo zegarka kieszonkowego, jest w naprawie u zegarmistrza, a ścienny mój zegar stanął. Udaję się więc do znajomego, u którego — jak wiem — zegary zawsze doskonale chodzą, czas pewien spędzam u niego i wróciwszy do domu nastawiam swój zegar zupełnie dokładnie. Jakim sposobem mogłem tego dokonać, jeśli poprzednio nie wiedziałem, ile czasu potrzeba, by przejść z mego mieszkania do mieszkania mego znajomego?
Zadanie sprowadza się do tego, by ustalić dokładnie godzinę po mym powrocie do domu. Otóż bezpośrednio przed wyjściem z domu nakręcam swój zegar, nastawiam go na którąkolwiek godzinę; godzinę tę oznaczam literą a. Natychmiast idę do znajomego i zaraz po przyjściu do niego notuję, która godzina jest na jego zegarze; oznaczam tę godzinę literą b.
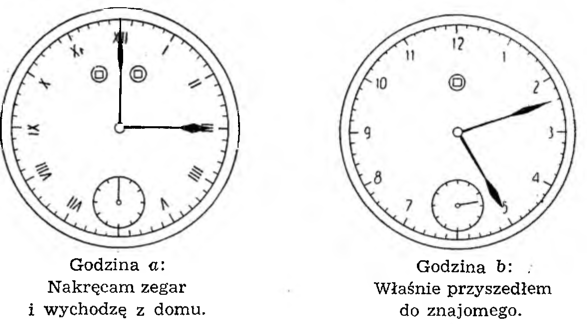 Pogawędziwszy ze znajomym (.. . i napiwszy się czarnej kawy) ustalam tuż przed wyjściem, która jest godzina według jego zegara; niech to będzie godzina c. Wróciwszy do domu stwierdzam, którą godzinę wskazuje mój zegar nastawiony na chybił trafił; niech to będzie godzina d.
Pogawędziwszy ze znajomym (.. . i napiwszy się czarnej kawy) ustalam tuż przed wyjściem, która jest godzina według jego zegara; niech to będzie godzina c. Wróciwszy do domu stwierdzam, którą godzinę wskazuje mój zegar nastawiony na chybił trafił; niech to będzie godzina d.
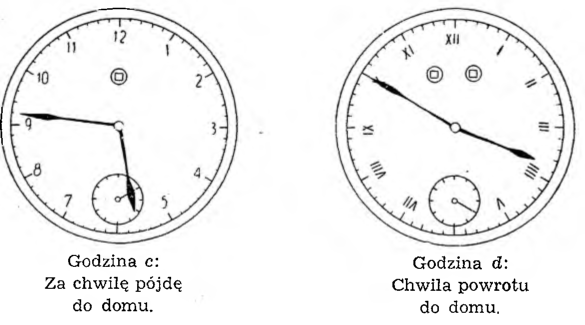 Wracając do domu miałem już przygotowany plan postępowania, więc w minutę po moim powrocie zegar mój wskazywał już prawidłową godzinę; była to godzina e.
Wracając do domu miałem już przygotowany plan postępowania, więc w minutę po moim powrocie zegar mój wskazywał już prawidłową godzinę; była to godzina e.
 A oto obliczenia:
A oto obliczenia:
Różnica d — a wskazuje, ile czasu byłem poza domem:
d — a = godz. 3 min. 50 — godz. 3 min. 00 = 50 min.
Różnica c — b wskazuje, ile czasu spędziłem u znajomego:
c — b — godz. 5 min. 46 — godz. 5 min. 12 = 34 min.
Różnica (d — a) — (c — b) wskazuje, ile czasu szedłem z mego domu do znajomego i z powrotem:
(d — a) — (c — b) = 50 min. — 34 min. = 16 min.
W obie strony starałem się iść krokiem równomiernym, więc mogę przyjąć, że na drogę powrotną zużyłem połowę tego czasu:
[(d – a) — (c — b)] / 2 = 8 min.
Dodawszy tę połowę do godziny c otrzymam dokładną godzinę w chwili mego powrotu do domu:
godz. 5 min. 46 + 8 min. = 5 godz. 54 min.
Dodałem jeszcze jedną minutę straconą na obliczenia — i oto mam dobry czas!