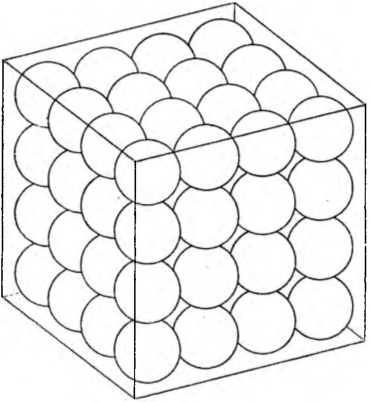
 Fabryka wysłała skrzynię sześcienną ze stalowymi kulkami. Pusta skrzynia ważyła 2 kg, a waga skrzyni brutto razem z kulkami wynosiła 18 kg. W skrzyni były 64 jednakowe kulki ułożone w czterech warstwach: na dole skrzyni leżała warstwa z czterech rzędów po cztery kulki, na niej druga taka sama warstwa, wyżej trzecia, wreszcie warstwa czwarta.
Fabryka wysłała skrzynię sześcienną ze stalowymi kulkami. Pusta skrzynia ważyła 2 kg, a waga skrzyni brutto razem z kulkami wynosiła 18 kg. W skrzyni były 64 jednakowe kulki ułożone w czterech warstwach: na dole skrzyni leżała warstwa z czterech rzędów po cztery kulki, na niej druga taka sama warstwa, wyżej trzecia, wreszcie warstwa czwarta.
W drugiej takiej samej skrzyni było 1000 kulek ułożonych w dziesięciu warstwach, a w każdej warstwie było dziesięć rzędów po dziesięć kulek w rzędzie. Ile ważyła ta skrzynia brutto?
Kulki w pierwszej skrzyni ważyły netto 16 kg, a ponieważ kulek było 64, więc każda kulka ważyła 0,25 kg.
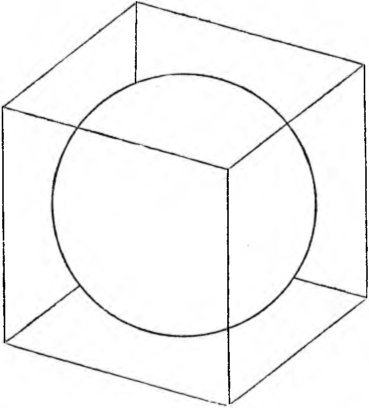
Zastanówmy się nad tym, ile ważyłaby jedna wielka kula, która dotykałaby wszystkich sześciu ścian skrzyni.
Kula taka miałaby średnicę 4 razy większą niż którakolwiek z 64 kulek przysłanych w pierwszej skrzyni. Ciężar tej kuli byłby 4 • 4 • 4 = 64 razy większy niż ciężar każdej z 64 kulek przysłanych w pierwszej skrzyni, a więc jedna wielka kula ważyłaby właśnie tyle, co 64 kulki przysłane w pierwszej skrzyni, czyli 16 kg.
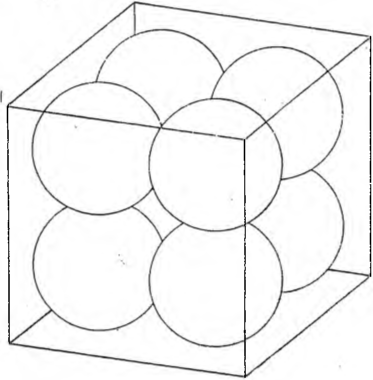 Jeżeli teraz weźmiemy kulki o średnicy 2 razy mniejszej niż średnica wielkiej kuli, to w skrzyni zmieści się 2 • 2 • 2 = 8 kul, łączny zaś ciężar będzie taki, jaki ma wielka kula!
Jeżeli teraz weźmiemy kulki o średnicy 2 razy mniejszej niż średnica wielkiej kuli, to w skrzyni zmieści się 2 • 2 • 2 = 8 kul, łączny zaś ciężar będzie taki, jaki ma wielka kula!
Gdybyśmy wzięli kule o średnicy 3 razy mniejszej niż średnica wielkiej kuli, to kul byłoby 3 • 3 • 3 = 27, łączny zaś ciężar zostałby ten sam.
Teraz możemy odpowiedzieć na pytanie, ile ważyła skrzynia z tysiącem kulek:
16 kg wagi netto, a 18 kg wagi brutto.
Na zakończenie oblicz, ile ważyłaby taka skrzynia, gdyby była napełniona stalowym śrutem ułożonym równymi warstwami!