 A. Ile razy w ciągu 12 godzin wskazówka minutowa stanie ponad wskazówką godzinową?
A. Ile razy w ciągu 12 godzin wskazówka minutowa stanie ponad wskazówką godzinową?
Dwanaście razy? Nie, tylko jedenaście! Pierwszy raz wskazówka minutowa dogoni godzinową o godzinie 1 minut 5 i 5/11. Za każdą też dalszą godziną będzie musiała wskazówka minutowa przebiec całą tarczę i 5 i 5/11 minuty. Drugie spotkanie nastąpi o godzinie 2 minut 10 i 10/11, trzecie o godzinie 3 minut 16i 4/11 i tak dalej, wreszcie jedenaste — o godzinie 11 minut 59 11/11, czyli ściśle o godzinie 12.
B. Jeśli zegar ścienny wybija godzinę VI w ciągu sześciu sekund, to ile czasu zużyje na wybicie godziny XII?
Każdy skłonny jest zrazu odpowiedzieć, że zużyje na to dwanaście sekund — zapominając, iż pomiędzy uderzeniem pierwszym a szóstym jest pięć pauz, gdy tymczasem pomiędzy szóstym a dwunastym uderzeniem takichże odstępów jest sześć. Zegar więc godzinę dwunastą bić będzie przez 13 i 1/5- sekundy. Zakładamy przy tym, że uderzenia zegara nie trwają, lecz są momentalne, są chwilą.
C. Posiadam — powiada jeden z matematyków — stary zegar ścienny, który wybija tylko pełne godziny. Nakręcać go muszę, niestety, codziennie; czynię to. po wybiciu godziny dwunastej w południe. W przeciągu doby oba ciężarki zegara opuszczają się jednakowo, każdy o 312 oczek łańcuszka.
Pewnego dnia podciągnąwszy ciężarki zegara wyszedłem z domu i po powrocie zauważyłem, że zegar wybił tyle razy, o ile oczek jeden ciężarek był wyżej od drugiego. Zastanowiło mnie, czy na podstawie tej jedynie okoliczności mógłby ktoś dojść, o której mianowicie godzinie powróciłem. Czy jest to zadanie rozwiązalne?
Owszem. Ciężarek powodujący chód zegara opuszcza się na godzinę oczywiście o 312:24= 13 oczek. A jak się zachowuje drugi ciężarek, który opada przy biciu zegara?
W ciągu dwunastu godzin zegar wybija godziny:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12.
Aby szybko obliczyć sumę dwunastu kolejnych liczb naturalnych zaczynając od jedności, należy ostatnią liczbę, więc liczbę 12, pomnożyć przez następną liczbę naturalną, czyli przez 13, i wynik mnożenia podzielić przez 2.
W naszym przypadku otrzymamy
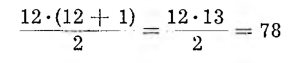 A więc w ciągu pół doby zegar wybije 78 razy, a w ciągu całej doby 156 razy. Ciężarek powodujący bicie zegara opuszcza się za każdym uderzeniem o 312 : 156 = 2 oczka łańcuszka.
A więc w ciągu pół doby zegar wybije 78 razy, a w ciągu całej doby 156 razy. Ciężarek powodujący bicie zegara opuszcza się za każdym uderzeniem o 312 : 156 = 2 oczka łańcuszka.
Skoro więc w chwili powrotu właściciela zegar wybił x razy, to od godziny dwunastej zegar wybił uderzeń
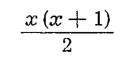 i w tym okresie ciężarek uruchamiający bicie zegara obniżył się o x(x+1) oczek łańcuszka, natomiast ciężarek poruszający wskazówki zegara obniżył się o x • 13 oczek.
i w tym okresie ciężarek uruchamiający bicie zegara obniżył się o x(x+1) oczek łańcuszka, natomiast ciężarek poruszający wskazówki zegara obniżył się o x • 13 oczek.
W myśl warunków zadania różnica między wyżej podanymi liczbami wynosiła właśnie x. Stąd równanie
13 x — x (x + 1) = x
Liczba x nie jest zerem. Dzieląc wszystkie wyrazy naszego równania przez x otrzymujemy prostsze równanie:
13-(x+l) = 1,
z którego znajdujemy x — 11.
Powrót do domu nastąpił o godzinie 11 wieczorem.
D. Dwa zegary A i B bijąc równocześnie wybiły 19 razy. Jak określić godzinę, którą wskazywały, skoro wiadomo, że początek bicia godziny na zegarze A spóźnił się w stosunku do zegara B o 2 sekundy i że zegar A uderza co 3 sekundy, a zegar B co 4 sekundy?
Przypuśćmy, że po raz pierwszy zbiegnie się n-te uderzenie zegara A z n-tym uderzeniem zegara B. Do tego momentu zegar A bił przez
(n — 1) • 3 sekundy, a zegar B bił przez (n — 1) • 4 sekundy.
Otrzymujemy równanie
(n — 1) • 4 — (n — 1) • 3 = 2 , z którego znajdujemy n = 3.
A więc trzecie uderzenie zegara A zbiega się z trzecim uderzeniem zegara B, a przedtem słychać było 2 uderzenia zegara B i 2 nieco opóźniające się uderzenia zegara A. Jeśliby więc zegary biły godzinę trzecią, to razem słychać by było 5 uderzeń.
W ciągu następnych 12 sekund zegar A wybije 4 razy, a zegar B tylko 3 razy, przy czym w ciągu tych 12 sekund usłyszymy 3 osobne uderzenia zegara A i 2 osobne uderzenia zegara B oraz 1 uderzenie łączne; to siódme uderzenie zegara A zbiegnie się z szóstym uderzeniem zegara B. Razem w ciągu 12 sekund usłyszymy 3 + 2 +1 — 6 uderzeń, co z poprzednimi 5 uderzeniami daje 11 uderzeń.
Ale musimy „dojechać” do 19 uderzeń. Dalsze 12 sekund dają znowu 3 osobne uderzenia zegara A i 2 osobne uderzenia zegara B oraz 1 uderzenie łączne; wtedy zegar A będzie bił po raz jedenasty, a zegar B po raz dziewiąty. Razem z poprzednimi 11 uderzeniami usłyszymy 17 uderzeń, a potem jeszcze co 4 sekundy słyszeć będziemy 2 opóźnione uderzenia zegara B: dziesiąte i jedenaste. Była więc godzina jedenasta.
Oto rozkład uderzeń zegarów w czasie:
