Pewien sprzedawca zauważył, że zwykła waga szalkowa, którą się posługiwał, ma jedno ramię dłuższe, nie daje więc właściwego ciężaru. Postanowił oczywiście odesłać wagę do naprawy; tak się jednak złożyło, że musiał wpierw jeszcze odważyć kupującemu pewną ilość towaru. Nie chcąc odważyć za dużo ani też za mało, postanowił odważyć połowę na jednej szalce, a drugą połowę na drugiej szalce.
Pewien sprzedawca zauważył, że zwykła waga szalkowa, którą się posługiwał, ma jedno ramię dłuższe, nie daje więc właściwego ciężaru. Postanowił oczywiście odesłać wagę do naprawy; tak się jednak złożyło, że musiał wpierw jeszcze odważyć kupującemu pewną ilość towaru. Nie chcąc odważyć za dużo ani też za mało, postanowił odważyć połowę na jednej szalce, a drugą połowę na drugiej szalce.
Gdy tak dowcipnym, jak mu się zdawało, pomysłem chwalił się przed pewnym matematykiem, ten po chwili namysłu musiał sprostować jego błędne mniemanie. Uczciwy sprzedawca bowiem wydał za dużo towaru.
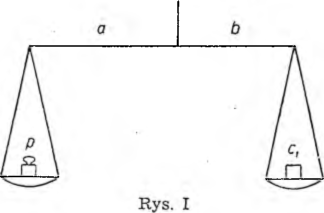 Oznaczamy owe różne długości ramion wagi przez a i b. Otóż przy pierwszym ważeniu (rys. I) zamiast właściwej wagi towaru p kupujący otrzymał wagę
Oznaczamy owe różne długości ramion wagi przez a i b. Otóż przy pierwszym ważeniu (rys. I) zamiast właściwej wagi towaru p kupujący otrzymał wagę
c1 = a/b • p
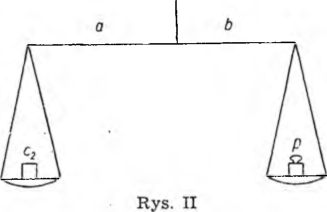
przy drugim zaś ważeniu (rys. II) otrzymał wagę
Sprzedawca tedy wydał razem towaru
(a/b + b/a) • p,
wziął zaś zapłatę za 2p. Jeżeli więc (a/b + b/a) > 2 to sprzedawca wydał za dużo towaru.
I tak właśnie być musiało, gdyż jeżeli a ≠ b, to (a — b)²> 0, stąd a² + b² > 2ab, czyli
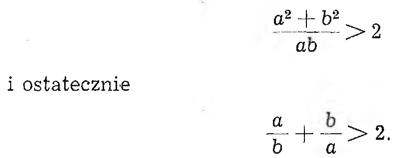 Tylko wtedy, gdyby a równało się b, sprzedawca wydałby średnią ilość towaru. Na fałszywej wadze można więc tylko albo nieuczciwie zyskać, albo uczciwie . .. stracić.
Tylko wtedy, gdyby a równało się b, sprzedawca wydałby średnią ilość towaru. Na fałszywej wadze można więc tylko albo nieuczciwie zyskać, albo uczciwie . .. stracić.