Figury magiczne dzielą się na płaskie i przestrzenne, są bowiem kwadraty, trójkąty, prostokąty, wielokąty i koła magiczne, ale są również i sześciany magiczne.
Kwadraty dzielą się: zależnie od postępu, w jakim idą liczby — na arytmetyczne i geometryczne; zależnie od podziałek boków — na nieparzyste (3, 5, 7, 9 i tak dalej), nieparzysto–parzyste (6, 10, 14, 18 i tak dalej) i parzysto-parzyste (4, 8, 12, 16 i tak dalej); zależnie wreszcie od ustawienia liczb w kwadracie — na magiczne zwykłe, magiczne o właściwościach szczególnych, hipermagiczne.
Kwadrat magiczny pozostanie magicznym, jeśli wszystkie liczby, jakie zawiera, powiększymy lub zmniejszymy o jedną i tę samą liczbę. Pozostanie również magicznym, gdy pomnożymy lub podzielimy wszystkie jego składniki przez jakąś liczbę stałą. Dla jasnego zrozumienia wystarczy przedstawić to na jednym przykładzie:
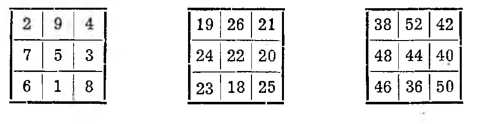 W pierwszym kwadracie suma magiczna, czyli suma liczb poszczególnych rzędów, kolumn lub przekątnych, wynosi 15; w drugim kwadracie dodajemy do każdej liczby po 17 i suma magiczna wynosi 15 + 3 • 17 = 66; wreszcie w trzecim kwadracie mnożymy wszystkie wyrazy przez 2 i suma magiczna wynosi 2 • 66 = 132.
W pierwszym kwadracie suma magiczna, czyli suma liczb poszczególnych rzędów, kolumn lub przekątnych, wynosi 15; w drugim kwadracie dodajemy do każdej liczby po 17 i suma magiczna wynosi 15 + 3 • 17 = 66; wreszcie w trzecim kwadracie mnożymy wszystkie wyrazy przez 2 i suma magiczna wynosi 2 • 66 = 132.
II. Jeśli kwadrat jest magiczny dla jakiegoś postępu arytmetycznego, to będzie magiczny dla tak samo rozmieszczonego postępu arytmetycznego o innym wyrazie pierwszym i o innej różnicy. Tak np. w pierwszym z podanych kwadratów magicznych zamiast liczb:
1, 2, 3, 4, 5, 6, 7, 8, 9 można odpowiednio rozmieścić wyrazy postępu:
91, 96, 101, 106, 111, 116, 121, 126, 131.
Ze wszystkich tych prawideł wyciągnąć można niezmiernie ważną wskazówkę praktyczną, iż formując jakikolwiek kwadrat magiczny wystarczy zestawić go naprzód z liczb najprostszych, więc z liczb naturalnego ciągu: 1, 2, 3, 4, 5, . .., gdyż potem przez mnożenie, dzielenie, powiększanie łub zmniejszanie tych liczb można osiągnąć nieskończoną ilość kwadratów magicznych o najrozmaitszych sumach magicznych.
Dalszą niezmiernie ważną właściwością kwadratów magicznych jest to, że z dwu kwadratów możemy otrzymać trzeci przez sumowanie liczb stojących w analogicznych polach:
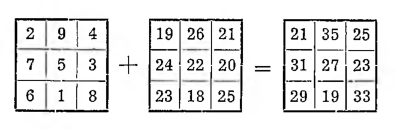 Suma magiczna takiego kwadratu równa się sumie sum magicznych obu składników: 81 = 15 + 66.
Suma magiczna takiego kwadratu równa się sumie sum magicznych obu składników: 81 = 15 + 66.
Kwadrat nie utraci swej magiczności, jeśli przestawimy jego kolumny oraz szeregi leżące symetrycznie względem środka kwadratu. Na przykład:
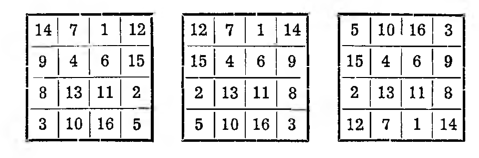 W pierwszym z tych kwadratów przestawiliśmy kolumny pierwszą i czwartą; powstał kwadrat drugi, w którym zachowała się suma wyrazów w każdym wierszu i w każdej kolumnie, ale nie zachowała się suma na przekątnych. Jeśli teraz w drugim kwadracie przestawimy wiersze pierwszy i czwarty, to otrzymamy kwadrat trzeci, już doskonale magiczny.
W pierwszym z tych kwadratów przestawiliśmy kolumny pierwszą i czwartą; powstał kwadrat drugi, w którym zachowała się suma wyrazów w każdym wierszu i w każdej kolumnie, ale nie zachowała się suma na przekątnych. Jeśli teraz w drugim kwadracie przestawimy wiersze pierwszy i czwarty, to otrzymamy kwadrat trzeci, już doskonale magiczny.