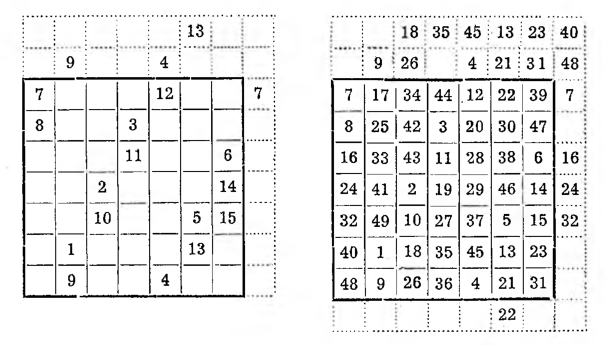
 IV. Metoda La Louber’a. Pokażemy ją na kwadracie rzędu piątego. Zamiast piramidek dobudowuje się do kwadratu głównego cztery inne kwadraty tejże wielkości, przez co otrzymuje się figurę podaną obok.
IV. Metoda La Louber’a. Pokażemy ją na kwadracie rzędu piątego. Zamiast piramidek dobudowuje się do kwadratu głównego cztery inne kwadraty tejże wielkości, przez co otrzymuje się figurę podaną obok.
W środkowym polu lewej kolumny wpisujemy 1 i idąc na ukos na prawo ku górze wpisujemy liczby 2, 3, 4, 5.
Po wpisaniu pierwszej piątki zatrzymujemy się.
Liczby 4 i 5 wyszły poza ramki kwadratu. Gdy każdą z nich przesuniemy o 5 pól w dół, wówczas znajdą się one wewnątrz kwadratu (obacz gotowy kwadrat na następnej figurze).
Pod tym nowym położeniem liczby 5 wpisujemy 6 i znowu idąc na prawo ku. górze wpisujemy 7, 8, 9, 10, Po wpisaniu drugiej piątki widzimy, że liczby 7, 8, 9, 10 wyszły poza ramki kwadratu; wprowadzamy je do kwadratu za pomocą przesunięcia o 5 pól w lewo. Pod nowym położeniem liczby 10 wpisujemy 11 i dalej 12, 13, 14, 15.
Aby umieścić w kwadracie liczby 13, 14, 15, trzeba będzie przesunąć je o 5 pól w dół i o 5 pól na lewo. Tak postępujemy do końca.
 Gdy dojdziemy do ostatniego wyrazu postępu, czyli, jak w danym razie, do 25, wówczas wszystkie liczby stojące w kwadratach dodatkowych przenosi się na analogiczne pole kwadratu głównego i otrzymuje się kwadrat magiczny odmienny od poprzedniego, otrzymanego metodą Bacheta. Pod polem 25 będzie pole 1.
Gdy dojdziemy do ostatniego wyrazu postępu, czyli, jak w danym razie, do 25, wówczas wszystkie liczby stojące w kwadratach dodatkowych przenosi się na analogiczne pole kwadratu głównego i otrzymuje się kwadrat magiczny odmienny od poprzedniego, otrzymanego metodą Bacheta. Pod polem 25 będzie pole 1.
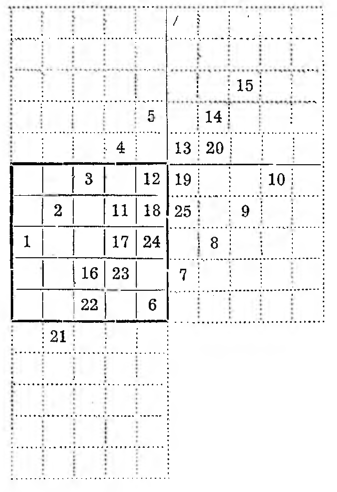
V. Pewna odmiana poprzedniej metody. Natchnieni myślą La L o u b e r e’a podajemy pewną odmianę jego metody dającą symetryczne kwadraty magiczne rzędu piątego. Otóż wypisujemy na papierze kratkowanym ciąg liczb tak rozmieszczony;
 Po wpisaniu wszystkich liczb do kratek wykreślamy grubszymi kreskami taki kwadrat, ażeby na jego przekątnej leżały liczby grupy podstawowej: 11, 12, 13, 14, 15, a następnie — w dostosowaniu do tego kwadratu — kreślimy grubszymi kreskami inne kwadraty rzędu piątego lub ich części.
Po wpisaniu wszystkich liczb do kratek wykreślamy grubszymi kreskami taki kwadrat, ażeby na jego przekątnej leżały liczby grupy podstawowej: 11, 12, 13, 14, 15, a następnie — w dostosowaniu do tego kwadratu — kreślimy grubszymi kreskami inne kwadraty rzędu piątego lub ich części.
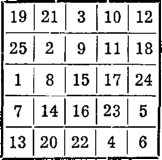
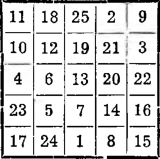 Teraz już nie trudno będzie przesunąć wszystkie liczby do wnętrza kwadratu głównego i otrzymać poszukiwany kwadrat magiczny. Jest to, jak łatwo stwierdzić, symetryczny kwadrat magiczny.
Teraz już nie trudno będzie przesunąć wszystkie liczby do wnętrza kwadratu głównego i otrzymać poszukiwany kwadrat magiczny. Jest to, jak łatwo stwierdzić, symetryczny kwadrat magiczny.
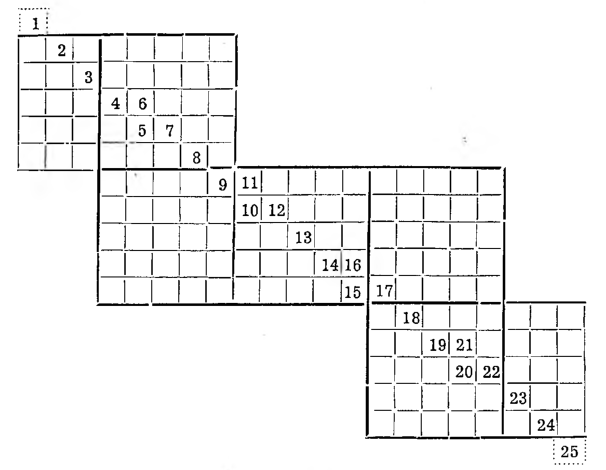
Kwadraty symetryczne mają ciekawą własność oryginalnego przeistaczania się w kwadraty innego typu. Mo^na mianowicie przesunąć drugi rząd liczb o jedną kratkę na prawo, potem trzeci rząd o dwie kratki na prawo i tak dalej, a następnie cały trójkąt wysuniętych liczb przerzucić do pustych kratek na lewo, jak to wskazuje schemat:
 Otrzymaliśmy znowu kwadrat magiczny, ale już niesymetryczny.
Otrzymaliśmy znowu kwadrat magiczny, ale już niesymetryczny.
VI. Metoda skoków konika szachowego, bardzo oryginalna, a zarazem łatwa i ciekawa. Weźmiemy tym razem dla przykładu znów kwadrat rzędu siódmego, czyli czterdziestodziewięciopolowy. Jedynkę stawiamy w którymkolwiek polu, nad nią zaś 2, 3 i tak dalej wpisujemy w polach, na które wypadłby skok konika szachowego. Czwórka wyjdzie już poza obręb kwadratu, należy więc ją przenieść na pole analogiczne wewnątrz kwadratu i dalej od niej kontynuować skoki. Gdy dojdziemy do siódemki, a potem do dalszych wielokrotności 7, to znaczy do 14, 21, . . ., liczbę następną, tj. 8, 15, 22, . . . podpisujemy w polu bezpośrednio niższym i od niej znów skokami konika rozstawiamy dalsze liczby, dopóki nie dojdziemy do 49.