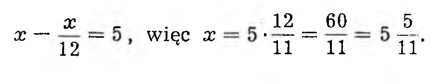Punktualnie o północy lub w południe obie wskazówki zegara stoją ponad godziną 12. W godzinę później wskazówka godzinowa stanie na liczbie 1, a minutowa będzie nad liczbą 12. Gdy minutowa wskazówka dojdzie do liczby 1, godzinowa przesunie się naprzód o 5/12 podziałki minutowej; gdy minutowa wskazówka dojdzie już do tego punktu (po upływie 5 i 5/12 min. od początku godziny), wskazówka godzinowa znów przesunie się dalej — i tak można ciągnąć w nieskończoność.

A więc właściwie wskazówka minutowa, „zasadniczo” i „teoretycznie” — nie powinna by wyprzedzić ani nawet dogonić wskazówki godzinowej!

Jak ten paradoks wyjaśnić?

W owym wyścigu wskazówek, podobnie jak w wyścigu Achillesa z żółwiem, rzecz cała polega na tym, że kolejne przesunięcia wskazówki minutowej dają szereg geometryczny nieskończenie malejący, mianowicie

Pierwszy wyraz tego postępu jest a = 5, iloraz q = 1/12

Skoro zaś, jak wiadomo, suma szeregu geometrycznego nieskończenie malejącego wyraża się wzorem
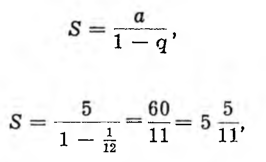a więc o godzinie 1 minut 5 i 5/11 wskazówki zejdą się w tym dniu po raz pierwszy, licząc od południa albo od północy.

Ale oto jeszcze jedno drobne potwierdzenie tego wywodu: Powiedzmy, że wskazówka minutowa dogoni wskazówkę godzinową w czasie x minut po godzinie 1. Droga, którą w tym czasie przejdzie wskazówka godzinowa, równa się oczywiście x/12. Kąt, który zakreśli „minutówka”, jest o 5 minut większy od kąta, który przejdzie „godzinniczka“. Stąd